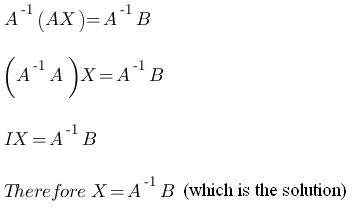Using the Matrix Inverse Method
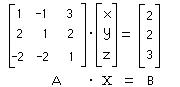
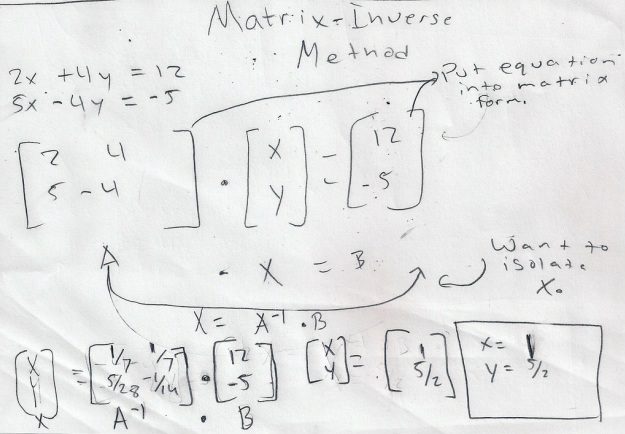
The matrix inverse method is very simple and easy to do. Basically, you change the system into one matrix equation. You first have to isolate the variables in the equation and put them onto the same side. Then you make a 2x2 or a 3x3 matrix depending on the number of variable in your system. For this explanation I will use a 2 equation system, because its easier. Anyway, Then you plug in the coefficients in the matrix. Each column is reserved for its own variable. For example, the left column is reserved for the coefficient of the x variable, and the right collumn is for the y variable. So, if you are writing the coefficient of the x variable in the first equation, you would plug it in the 1st row 2nd column. Let's call this matrix 'A'. Next you multiply this matrix with a 2x1 matrix or 3x1 matrix again depending on the number of equations in your system. You label the top component 'x' and the bottom component 'y', and if you have a three equation system you label the bottom component 'z'. This matrix will be named 'X'. Then you make the resulting matrix. It is either a 1x2 or a 1x3 matrix, again depending on the # of equations in your system. This is where you put your products to the equations in your system. The top component will be for the 1st equation's product and the bottom component will be for the 2nd equation's product. Let' name this Matrix 'B'. After you set up the Matrix equation, you have to find the inverse of the Matrix A. This will allow you to isolate the X matrix, so you can solve for the variables. After finding the inverse, you have to multiply the inverse of A by B.